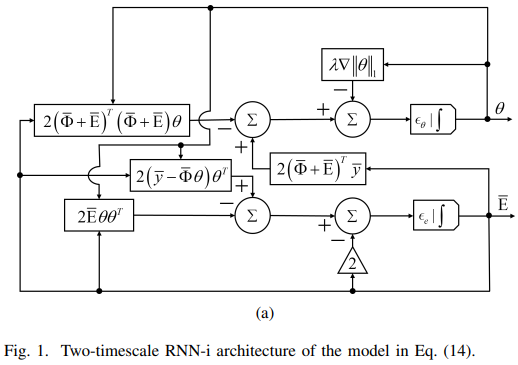
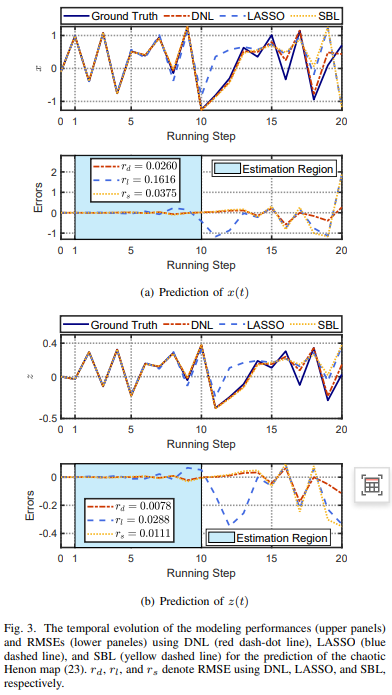
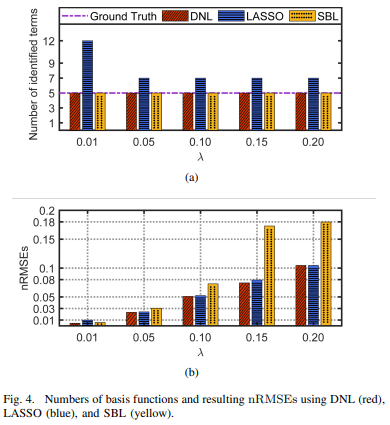
Abstract—Data-based discovery of the underlying dynamics of nonlinear systems is of great importance to the prediction and control of engineering systems. This paper presents a duplex neurodynamic learning (DNL) approach to the identification of discrete-time nonlinear systems subjected to both external disturbances and measurement noise. A neurodynamic learning method is proposed based on two-timescale recurrent neural networks (RNNs) for system identification. Truncated singular value decomposition is adopted to purify the data contaminated by external disturbances and measurement noises. Two RNNs are employed to cooperatively search for a global optimal solution, and the particle swarm optimization rule is used to reinitialize the RNNs upon the local convergence of the RNNs. The effectiveness and superiority of the proposed DNL method are demonstrated via simulations on benchmark chaotic and NARMAX systems.