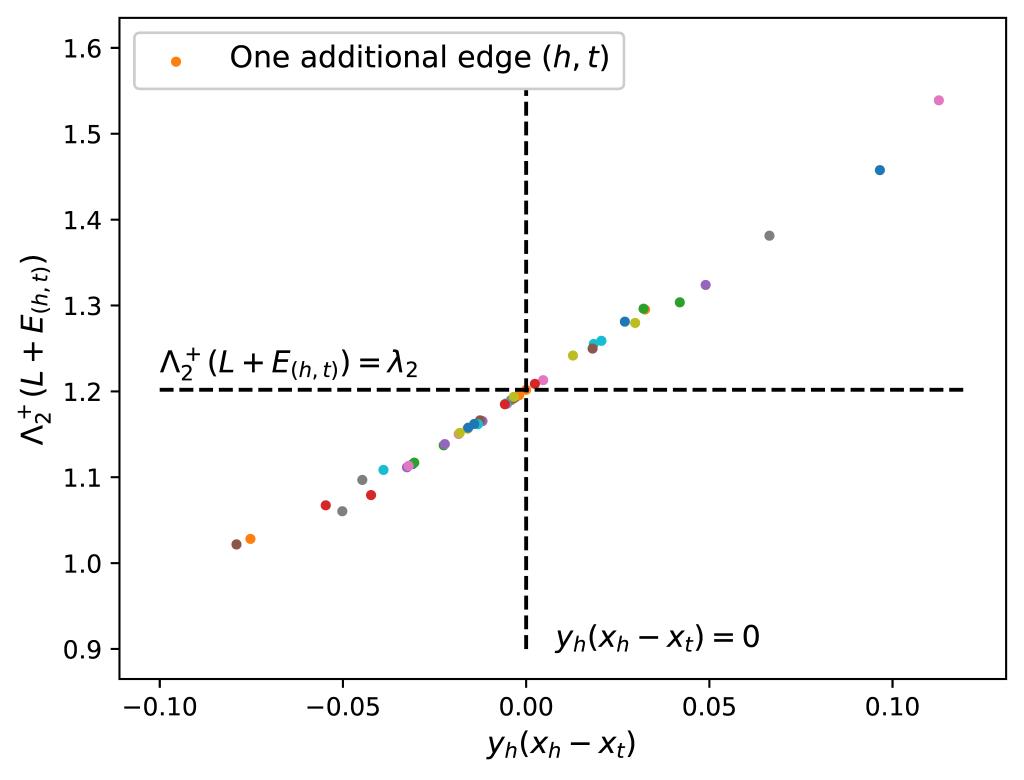
Abstract:Distributed networked systems with Laplacian dynamics play a crucial role in various fields such as engineering, biology, system science, social science and physics. To optimize the synchronization performance of such networks, topological adjustments have been identified as effective and efficient ways. This paper establishes a theoretical framework for accelerating synchronization convergence by introducing an additional directed edge or increasing edge weight to a network topology. The convergence speed is quantified by the second smallest real part of Laplacian matrix eigenvalues, called Fielder eigenvalue. We develop a necessary and sufficient condition guaranteeing synchronization acceleration with additional edge of single-root digraphs, enabling efficiently screening out all such edges through computation of graph Laplacian eigenspace. Moreover, for a sufficiently small topological variation, the accelerating extent and optimal edge can be approximately estimated as well. Numerical examples demonstrate the effectiveness of the proposed identification method of acceleration edges.